Polynomial Root Calculator | How to Find Root of a Polynomial?

Created By : Rina Nayak

Reviewed By : Rina Nayak

Last Updated : Apr 15, 2023

Free Polynomial Root Calculator determines the roots of a polynomial in a fraction of seconds. Just enter the polynomial expression details in the below-mentioned input field of the calculator and tap on the calculate button. The polynomial roots with explanation will appear on the screen as output.

Ex:

Use '^' for exponent

Here are some samples of Polynomial Root calculations.

Polynomial Root Calculator: Roots of a Polynomial Calculator: Are you trying to find the polynomial equation roots and don’t know the easier method? Then we are here to help you out in obtaining the roots of the polynomial. This online Root Polynomial Calculator tool assists you to understand the process to calculate the polynomial roots.

What is meant by Polynomial Root?

Roots are the solutions of the polynomial equation and these are the values of the unknown variable. The equation with a degree of 2 is called a quadratic equation and it is in the form of ax² + bx + c = 0. In the above equation, a, b, c are the coefficients and x is the variable. The solution of variable x can be known by finding the roots of the quadratic equation. The formula of the quadratic equation roots is given as: x = [-b ± √(b² − 4ac)]/(2a) The formula to find the roots of the linear polynomial i.e ax + b is x = -b/a.

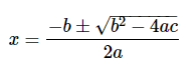
Steps to Calculate Polynomial Roots

The following are the steps to compute the polynomial root easily. Have a look at these simple steps and get the result.

1. Know the highest degree polynomial equation.

2. Apply either the quadratic equation formula or linear polynomial formula based on the degree of polynomial.

3. Substitute the values in the selected formula

4. Solve the problem and get the root value

Also, You can use our site ie., factorpolynomials.com provided a trusted and reliable best calculator ie., Polynomial Root Calculator for all your complex calculations & make them easy & simple when your polynomials_calculatorwork or assignments.

Polynomial Root with Example

Example

Question: Find the roots of polynomial 14x² + 42x + 70..

Solution:

The given polynomial is 14x² + 42x + 704

After factoring we get 14(x² + 3x + 5)

By expanding the summation:

Polynomial Roots Calculator is a set of methods aimed at finding values of x for which F(x)=0

So, x² + 3x + 5 = 0

The coefficients of above quadratic equation are a = 1, b = 3 and c = 5

The formula of quadratic equation root is x = [-b ± √(b² − 4ac)]/(2a)

x = [-3 ± √(3² − 4 * 1 * 5)]/(2 * 1)

= [-3 ± √(9 − 20)]/2

= [-3 ± √-11]/2

= [-3 + √11 i]/2 or [-3 - √11 i]/2

Therefore, the roots of polynomial 14x² + 42x + 70 are [-3 + √11 i]/2 or [-3 - √11 i]/2.

FAQs on Polynomial Root Calculator

1. How do you find the roots of a polynomial?

The steps to find the polynomial roots are given here. Make the equation P(x) = 0 by putting each factor value equal to 0 and solving for x.

2. How to get the discriminant?

The formula to find the discriminant of a 2nd order polynomial is Δ = b² − 4ac. So, use this formula and substitute the values to obtain the discriminant of the equation

3. What is meant by the polynomial equation?

In mathematics, a polynomial equation is defined as the algebraic equation that has variables, coefficients, constants, mathematical operators. A polynomial equation can have many terms with different exponents. The higher exponent value of the variable is called the degree of the equation.

4. Find the roots of the polynomial equation 15x² + 8x + 3?

Given polynomial equation is 15x² + 8x + 3 It is a quadratic equation in the form of ax² + bx + c. So, a = 15, b = 8, c = 3 The formula to find the roots of the quadratic equation is x = [-b ± √(b² − 4ac)]/(2a) x = [-8 ± √(8² − 4 * 15 * 3)]/(2 * 15) = [-8 ± √(64 − 180)]/(30) = [-8 ± √(-116)]/(30) = [-8 + √116i]/(30) and [-8 - √116i]/(30)